ホーム > 特集
特集
量子コンピュータの概要と研究内容

はじめに

近年、量子コンピュータに関する研究開発が,ソフトウェア・ハードウェアの双方で著しい進展を遂げている。量子コンピュータとは、量子力学を本質的にその計算原理に組み込んだコンピュータのことであり、スーパーコンピュータを含む古典コンピュータ(ここで古典とは、古典力学に基づいていることを意味している)よりも高速に問題が解けると期待されている。その実現は不可能とされていた時期もあったが、今はそうではない。今日(2024年1月26日時点)では、IBMが127量子ビットを備えるIBM製量子コンピュータを、クラウドサービスによって無料公開しており、身近なものになっている。本記事では、執筆者の研究分野でもある量子コンピュータの概要と、執筆者の研究内容を紹介する。
量子コンピュータの概要
量子コンピュータの概要を、歴史を踏まえて紹介する。量子コンピュータの発端は、1982年にR.P. Feynmanが、量子系のシミュレーションは、量子力学に基づいたコンピュータで行うべきと指摘したこと[1]だとされている。量子系のシミュレーションは物質科学や創薬の分野にて非常に重要であり、今日でも研究が続けられている。その後、1985年にD. Deutschによって量子版のチューリングマシンが定式化[2]され、1992年には古典よりも高速であるDeutsch–Jozsaの量子アルゴリズムが示された[3]。
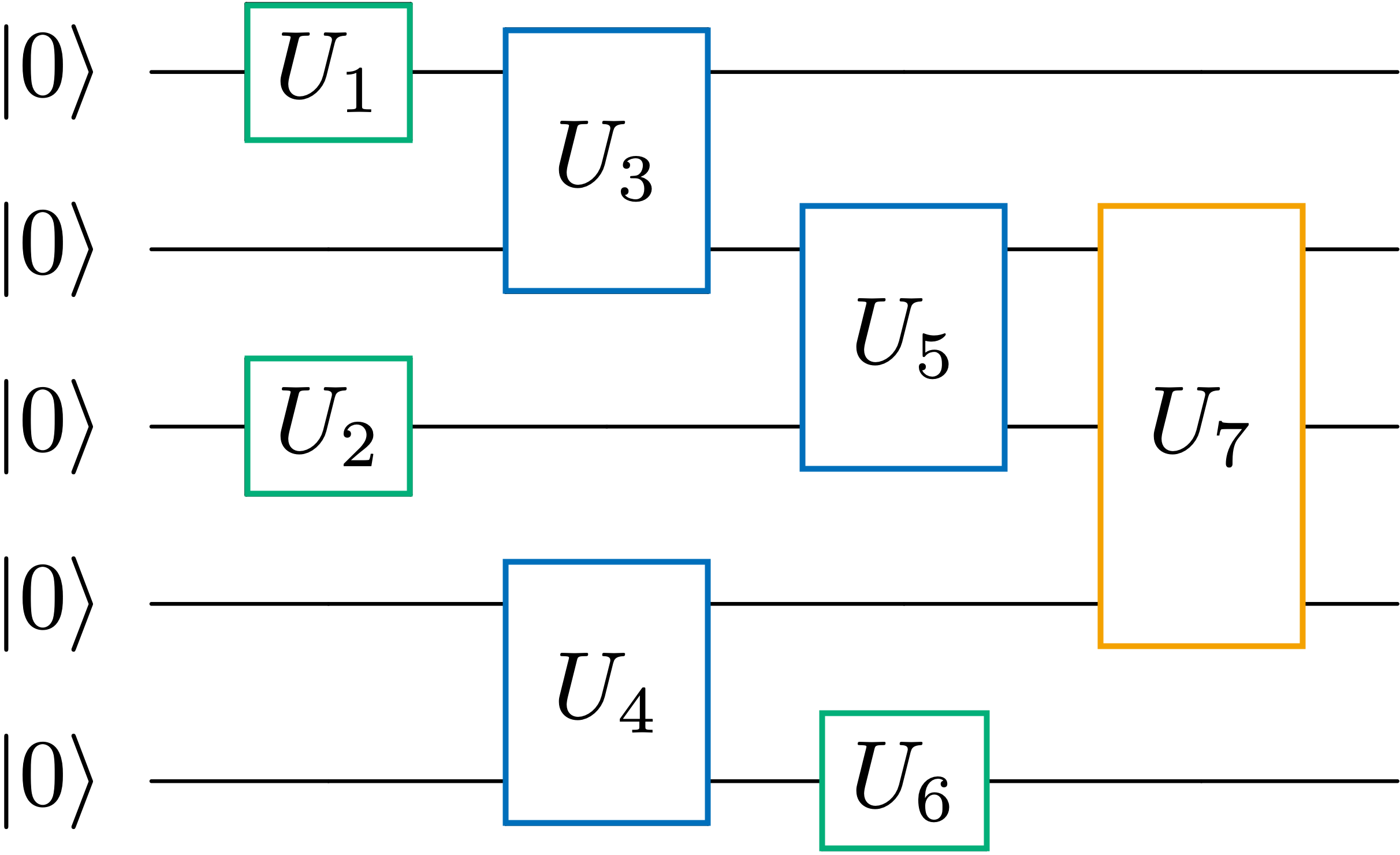
図1に量子コンピュータにおける計算過程を記述する量子回路を示す。このような量子回路をうまく構成することで、量子アルゴリズムを設計する。量子アルゴリズムの設計は、古典とは動作原理が異なること、また古典よりも高速であることを目標とするため、難しい問題である。
量子コンピュータが注目を集めたきっかけの一つは、1994年に発表されたShorの量子アルゴリズム[4]である。これは素因数分解を、知られている最良な古典アルゴリズムよりも指数関数的に高速に行う量子アルゴリズムであり、量子が古典を凌駕する可能性を秘めていることを現実的な問題で示したものである。素因数分解を効率的に解けれることは、広く使われているRSA暗号を簡単に解読できることを意味する。そのため注目を集め、量子暗号の研究や耐量子暗号の研究の進展に繋がった。その後、Groverの量子探索アルゴリズム[5]や線形方程式に対するHarrow-Hassidim-Lloyd(HHL)アルゴリズム[6]などの様々な量子アルゴリズムが提案された。特に、HHLアルゴリズムは、線形方程式という汎用性の高い問題を対象にしていることから機械学習へと応用され、量子機械学習という分野を構成するきっかけになった。
Shorの量子アルゴリズムの提案以降、量子コンピュータの有用さが認識され、実機の開発が進むようになった。2014年以降に大手IT企業・研究所が製作した、代表的な量子コンピュータの製作年と量子ビット数についてプロットしたグラフを図2に示す。2010年以前は数量子ビットが限界であったが、2014年にJ. Martinisのグループ(後にGoogleと連携)による超伝導量子ビットの製作以降、量子ビットの数は順調に増えている。このグラフが示すように、夢の技術と見なされてきた量子コンピュータは、実現しつつある。
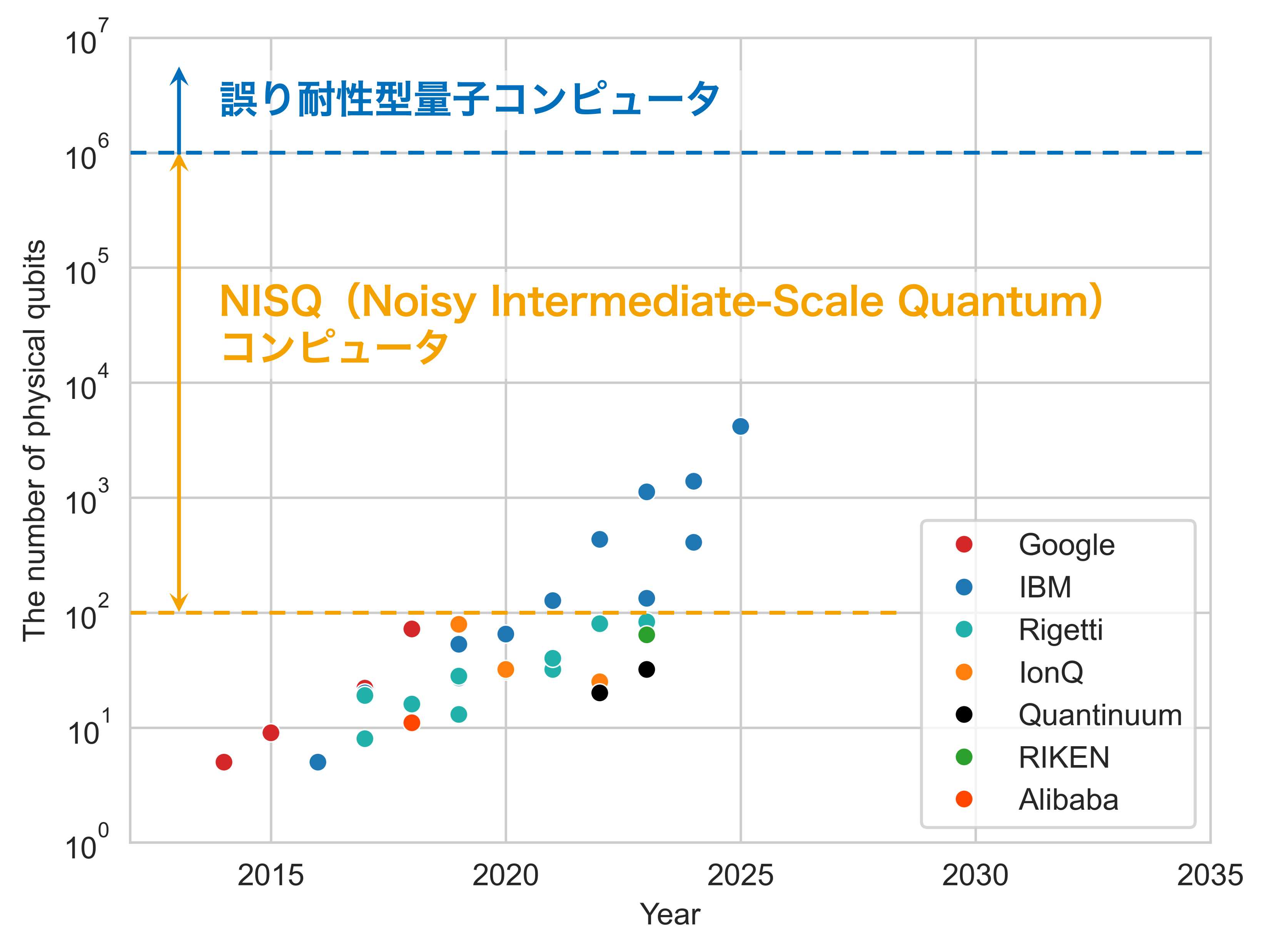
量子コンピュータは理論上のものから、実際に作って動かすという段階になっている。現時点のものは、エラーの影響を受けやすいが、小・中規模の量子ビットを持つもの(NISQ(Noisy Intermediate-Scale Quantum)コンピュータなどと呼ばれる)であリ、HHLアルゴリズムなどを動かすことができない。ただし、2019年にGoogleが行った量子超越性の実験が示唆するように、NISQコンピュータであっても古典コンピュータを凌駕する可能性がある。HHLアルゴリズムなどを動かすためには、大量の物理量子ビットによってエラーに対処できるよう冗長性を持たせた、誤り耐性型量子コンピュータの開発が必要不可欠である。そのためには、誤り訂正符号や、量子回路の最適化、制御システムの構築などが必要とされ、情報工学がより必要不可欠になってくる。量子コンピュータの実現・利活用のために、情報工学がより活躍することが期待されている。
研究内容の紹介:行列関数に対する量子アルゴリズム
執筆者の研究内容を紹介する。執筆者は量子アルゴリズムに興味を持っており、特に、線形方程式や固有値問題などの数値線形代数に関係する量子アルゴリズムの研究をしている。上記で述べたHHLアルゴリズムとは、密接に関係している。これまでに行列関数に対する量子アルゴリズムを提案してきた。以下で、より具体的に説明する。
複素関数\(f(z) = a_0 + a_1 z + a_2 z^2 + \cdots \ (z\in\mathbb{C}, a_i \in \mathbb{C})\)に対して、変数\(z\)を\(N \times N\)の行列\(A\)で置き換えたような行列\(f(A) = a_0 I + a_1 A + a_2 A^2 + \cdots\)は行列関数と呼ばれている。ここで\(I\)は単位行列である。行列関数は、線形方程式などと同様に、科学・工学・情報科学の様々な場面で現れる。例えば、行列指数関数(\(f(z) = \exp(z)\))は量子系のシミュレーションに現れ、ネットワークの解析などにも現れる。
行列関数に関する量子アルゴリズムを構成することは、このような背景から重要であり、多数の提案がされている。その中でも、量子特異値変換(QSVT)[7]は、単純な構成によって様々な行列関数を扱えるものであり、また、様々な量子アルゴリズムを統一的に記述できることから、大きな注目を集めている。QSVTで扱う行列関数は、一般化行列関数と呼ばれるもの、より具体的には、\(f(A) = Uf(\Sigma)V^\dagger\)と定義される行列である。ここで\(f(x)\)は実関数であり、\(A = U\Sigma V^\dagger\)は行列\(A\)の特異値分解を表す。そのため、\(A\)が非正規行列の場合は、行列関数を実行するような量子回路を表現できなかった。
そこで、次のような行列関数の積分表示に注目している。
$$ f(A) = \frac{1}{2\pi i}\int_\Gamma f(z)(zI - A)^{-1} dz $$ここで\(\Gamma\)は、行列\(A\)の全ての固有値を囲むような複素平面上の閉曲線である。数値積分を行うことで、次のような逆行列の線形結合を得る。
$$ \frac{1}{M}\sum_{k=0}^{M-1} f_i (z_i I - A )^{-1} $$ここで\(f_i\)や\(z_i\)は、数値積分の方法によって変わるようなパラメータ(複素数)である。なお、数値積分の方法としては、台形則やGauss-Laguerre積分、また二重指数関数型数値積分公式(DE公式)などがある。
このような積分表示の行列関数を、古典コンピュータ上で計算するには、\(z_i I - A\)を計算してから、逆行列を陽に計算し、そのまま足せば良い。しかし、量子コンピュータ上で計算するための、効率的な($N$について対数スケールのゲート計算量を持つような)量子アルゴリズムを設計することは、単純には難しい。
そこで我々は、Linear Combination of Unitaries (LCU) に基づくChilds-Kothari-Somma (CKS) アルゴリズム[8]と重みをかけるような量子回路をうまく組み合わせることで、閉曲線\(\Gamma\)が単位円である場合に、非正規行列であっても行列関数を実行できるような効率的な量子回路を構成した[9]。この構成は、CKSアルゴリズム が \(A\) に関するQRAMモデルを扱っていること、さらには非正規行列を係数とする線形方程式は、エルミート行列を係数とする線形方程式に、サイズを2倍にすることで帰着できることを利用している。
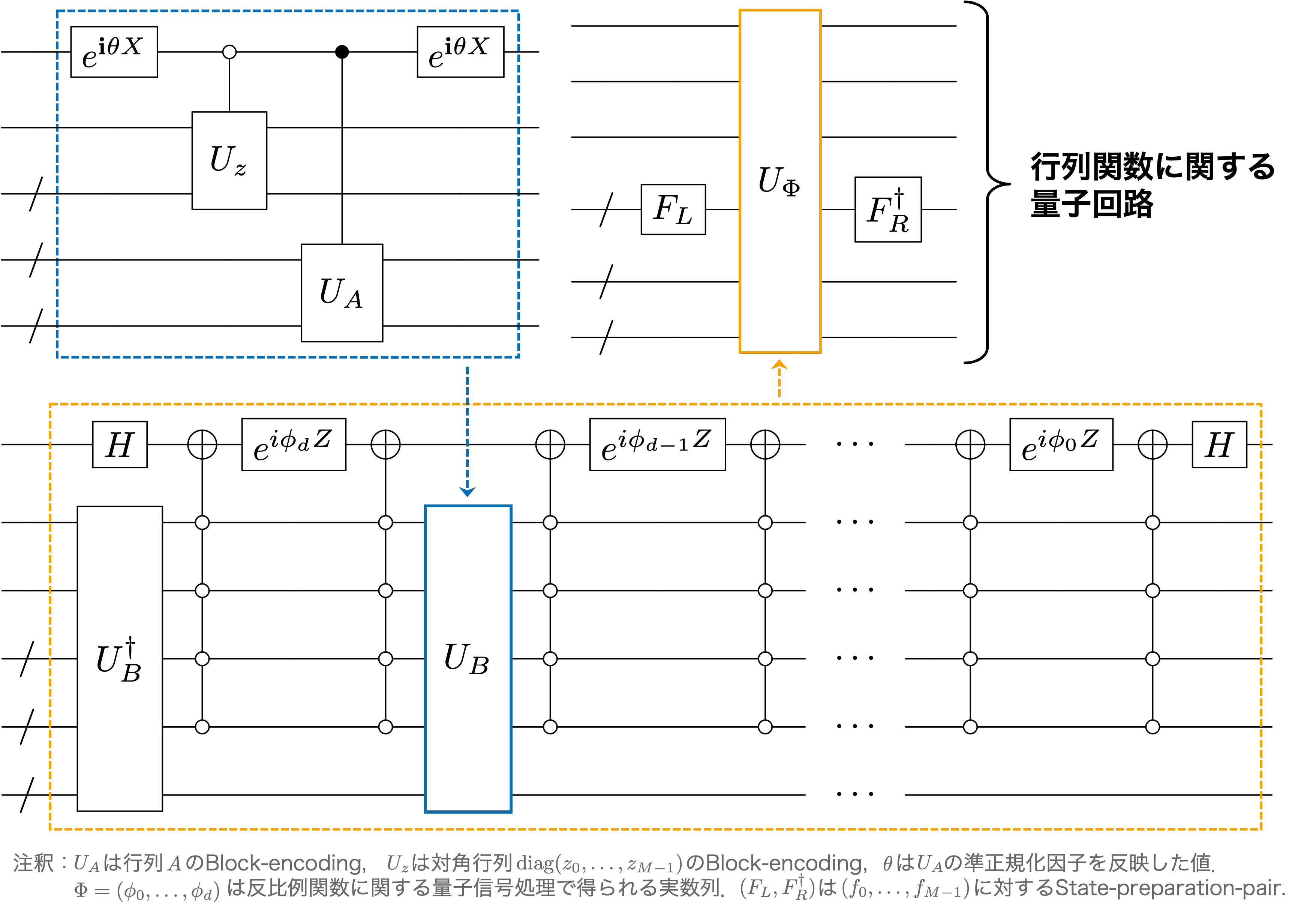
また、後の研究では、Block-encoding の枠組み[7]を利用した量子回路を構成した[10]。図3に構成した量子回路を示す。ここでは、LCUで用いられた線形結合を扱うための枠組みと、反比例関数に関するQSVTを組み合わせている。2020年の研究で構成した量子回路は非常に複雑であったが、Block-encodingを用いることで簡単な量子回路になった。最近の研究[11]では、行列対数関数や行列平方根などに注目し、提案した量子アルゴリズムの評価を数値的に行っている。
まとめ
量子コンピュータの概要と研究内容について紹介した。量子コンピュータは大きな注目を集めて盛り上がっている分野であり、今後も更なる発展が期待できる。本記事が量子コンピュータに、更には執筆者の研究内容に興味を持つきっかけになれば幸いである。
参考文献
1. R.P. Feynman, "Simulating physics with computers," Int. J. Theor. Phys., 21, pp.467-488, (1982).
2. D. Deutsch, "Quantum theory, the Church–Turing principle and the universal quantum computer," Proc. R. Soc. Lond. A, 400, pp.97–117, (1985).
3. D. Deutsch and R. Jozsa, "Rapid solution of problems by quantum computation," Proc. R. Soc. Lond. A, 439, pp.553–558, (1992).
4. P.W. Shor, "Algorithms for quantum computation: Discrete logarithms and factoring," Proc. 35th Ann. IEEE Symp. Found. Comput. Sci., pp.124-134, (1994).
5. L.K. Grover, "A fast quantum mechanical algorithm for database search," Proc. 28th ACM S. Theory Comput., pp.212-219, (1996).
6. A.W. Harrow, A. Hassidim, and S. Lloyd, "Quantum algorithm for linear systems of equations," Phys. Rev. Lett. 103, 150502, (2009).
7. A. Gilyén, Y. Su, G.H. Low, and N. Wiebe, "Quantum singular value transformation and beyond: exponential improvements for quantum matrix arithmetics," Proc. 51st ACM SIGACT S. Theory Comput., pp.193-204, (2019).
8. A.M. Childs, R. Kothari, and R.D. Somma, "Quantum algorithm for systems of linear equations with exponentially improved dependence on precision," SIAM J. Comput., 46, pp.1920-1950, (2017).
9. S. Takahira, A. Ohashi, T. Sogabe, and T.S. Usuda, "Quantum algorithm for matrix functions by Cauchy's integral formula," Quant. Inf. Comput., 20, No.1&2, pp.14-36, (2020).
10. S. Takahira, A. Ohashi, T. Sogabe, and T.S. Usuda, "Quantum algorithms based on the block-Encoding framework for matrix functions by contour integrals," Quant. Inf. Comput., 22, No.11&12, pp.0965-0979, (2022).
11. S. Takahira, A. Ohashi, T. Sogabe, and T.S. Usuda, "On the performance for the block-encoding of the matrix functions evaluated by the numerical quadrature method," 23rd Asian Quant. Inf. Sci., (2023).
